Convert Component Positions

Transcription:

In this video, I will show you that it is very easy to convert any position definitions and dependency definition of the elements even after the complete setup of the optical system.

For example, it is possible to convert between the option if this lens highlighted in red is positioned relative to the first lens or absolute to the global coordinate system, or maybe the lenses are stacked on each other in the same mounting and so on.

To set up the correct position dependencies is, of course, very important for accurate tolerancing results.

So after you’ve set up your optical system in the for you most convenient intuitive way, you can just convert afterwards all the dependencies without affecting and changing the positions of the elements.

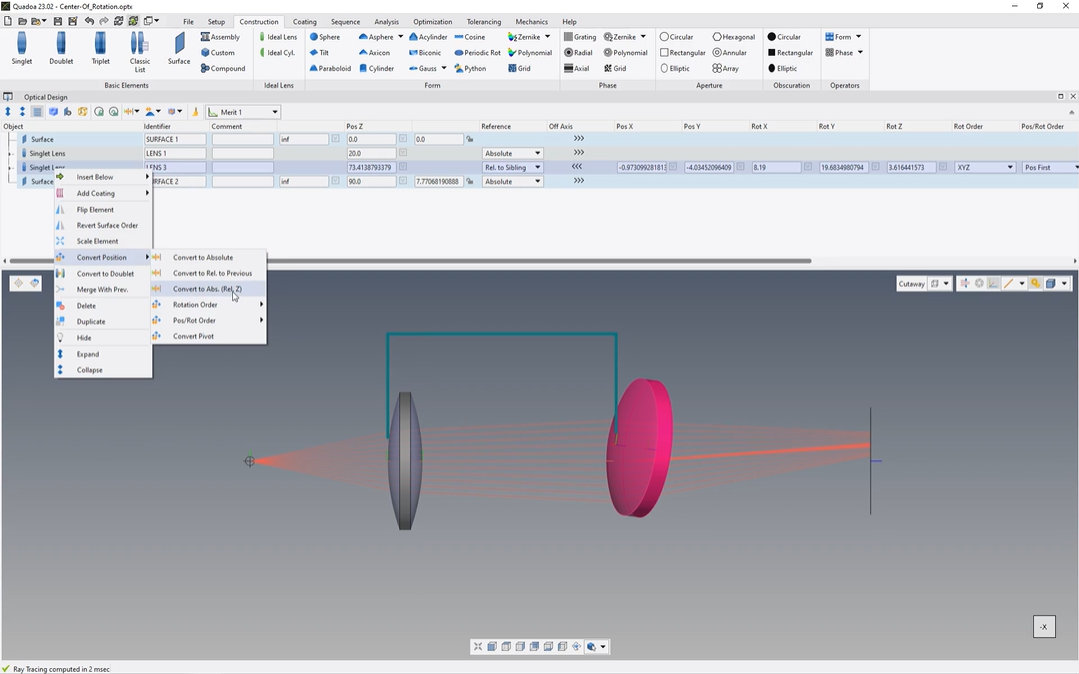
And as I mentioned, the correct definition of the dependencies of the lenses is, of course, of very high importance for accurate tolerancing results. And to convert the position definitions, we click in the optical design editor with the right mouse button on the lens for which we would like to convert the definition.

And in a drop down menu, we can see here this convert position, and there you have several options. For example, this convert to absolute.

As you can see here, this set value has been changed without affecting the position in our three-dimensional space.

Convert to relative to previous.

Again, the c value has changed without affecting the position in our three-dimensional space.

Convert to relative to sibling.

Convert to absolute in relation to set. With that option, only the c position is changing, and the settings especially of importance for correct tolerance analysis of, for example, stack mountings.

We can also convert the rotation order. The rotation order is, of course, also of great importance because it affects as well the position and the rotation of the lenses. Here we can convert if whether the lenses are first rotated and then positioned or the other way around. And here we have one option for converting the pivot point. In my case, we can see that the pivot point is minus one hundred fifty zero. And when I will rotate here this lens, we can see that it will rotate around this pivot point.

And when we change or convert the pivot point, for example, to zero zero zero, we can see that here the positions for x y in set and the rotation for x, y, and z has changed, but we again, without affecting here the positioning of the lens in the three-dimensional space.

And when rotating now, we can see that it will rotate around its own center because the pivot point is zero zero zero.

So as you can see, it is really easy to convert and redefine the position and dependencies of the lenses afterwards, not affecting and changing the positions of the elements. And this is very important for realistic tolerance results.

Thanks for watching.