Convert Surface Form Wizard

Convert Surface Form Wizard

Learn how to convert an aspheric surface from one type of polynomial to another.

Transcription:

In this tutorial, I will show you how we can convert a form description. For example, here this asphere into another form description.

For example, into a q type q b s f asphere.

And for that, we go here on this surface, which we would like to convert, and we click with the right mouse button on that. And then we can here select convert form, or we go here to the construction tab and under actions, we can find here this form. And there we also find this convert form wizard.

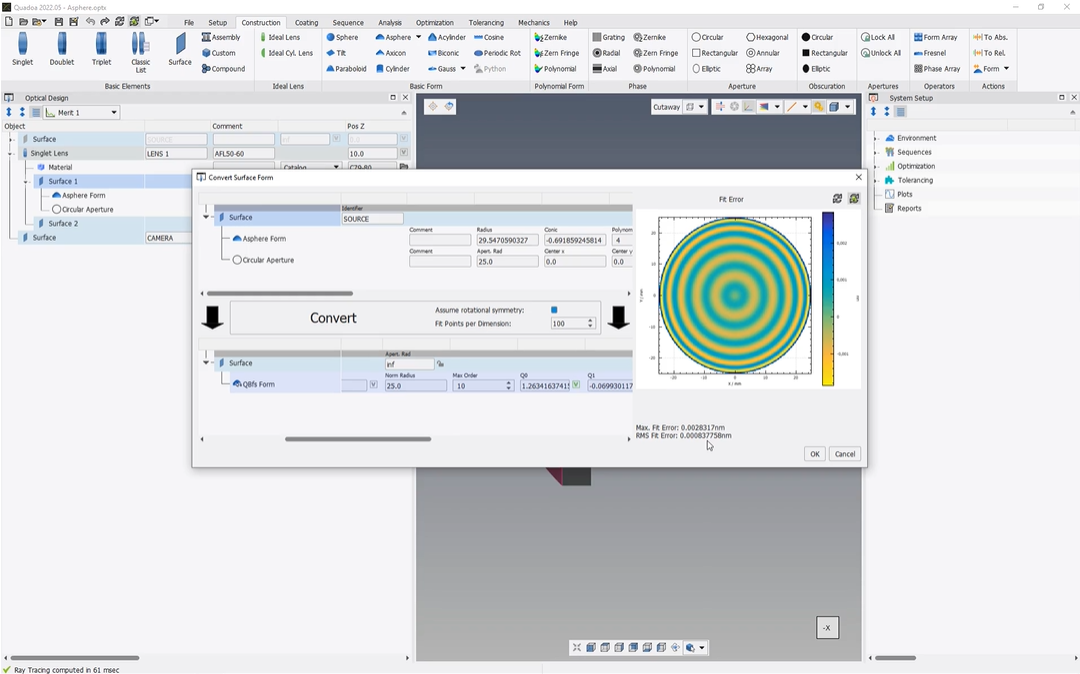
And when we open this convert surface form wizard, we can see that on the top, our old form is defined. So here in this case, our AC form.

And here on the bottom, we can add the new form which we would like to have instead of our a sphere.

So in my case, we click here with the right mouse button on add form, and then we just select the new form which we would like to have. So in my case, this a sphere q type q b f s.

And now we can further define the specifications for our new form.

I would like to set this radius to a variable, Our norm radius should be the same as our as the radius of our former asphere. So in my case, twenty five is here, the aperture radius.

And I would like to have ten polynomials.

And the polynomials should all be set to variable.

And for that, we click here just with the right mouse button and set all variable.

Since our form is rotationally symmetric, we can set the assume rotational symmetry checkbox.

And now we define our new form, and now we can click here on the convert button.

And now we see here on the right that we converted this asphere into this Q type BFS asphere.

And here we see our fitting error is something zero point zero zero nanometer, so that’s totally fine.

Now we click on the okay button, and now we see that here this QBFS form has been inserted.

So we have changed this former asphere into this QBFS form asphere without changing to the shape of this form. We’ve just changed here the description of our form.

Thank you for watching.